machine translation
enhacing machine translation using contextual parameter generation and curriculum learning
During my PhD I worked on a couple of interesting projects related to machine translation. In this page I plan to talk about two of them: one which introduced the idea of contextual parameter generation (CPG) and one which proposes a novel framework for curriculum learning and applies it to the problem of machine translation. The following post is currently about the first project, but it will soon be updated with information about the second.
NOTE: The following article has also appeared on the CMU machine learning department blog.

Figure 1: Overview of the contextual parameter generator that is introduced in this post. The top part of the figure shows a typical neural machine translation system (consisting of an encoder and a decoder network). The bottom part, shown in red, shows our parameter generator component.
Machine translation is the problem of translating sentences from some source language to a target language. Neural machine translation (NMT) directly models the mapping of a source language to a target language without any need for training or tuning any component of the system separately. This has led to a rapid progress in NMT and its successful adoption in many large-scale settings.

Figure 2: Illustration of the machine translation problem.
NMT systems typically consist of two main components: the encoder and the decoder. The encoder takes as input the source language sentence and generates some latent representation for it (e.g., a fixed-size vector). The decoder then takes that latent representation as input and generates a sentence in the target language. The sentence generation is often done in an autoregressive manner (i.e., words are generated one-by-one in a left-to-right manner).
Multilingual Machine Translation
It is easy to see how this kind of architecture can be used to translate from a single source language to a single target language. However, translating between arbitrary pairs of languages is not as simple. This problem is referred to as multilingual machine translation, and it is the problem we tackle. Currently, there exist three approaches for multilingual NMT.



Figure 3: Overview of existing approaches for multilingual neural machine translation.
Assuming that we have \(L\) languages and \(P\) trainable parameters per NMT model (these could be, for example, the weights and biases of a recurrent neural network) that translates from a single source language to a single target language, we have:
- Pairwise: Use a pairwise NMT model per language pair. This results in \(L^2\) separate models, each with \(P\) parameters. The main issue with this approach is that no information is shared between different languages, and even between models translating from English to other languages, for example. This is especially problematic for low-resource languages, where we have very little training data available, and would ideally want to leverage the high availability of data for other languages, such as English.
- Universal: Use a single NMT model for all language pairs. In this case, an artificial word can be added to the source sentence denoting the target language for the translation. This results in a single model with \(P\) parameters, since the whole model is shared across all languages. This approach can result in overfitting to the high-resource languages. It can also limit the expressivity of the translation model for languages that are more "different" (e.g., for Turkish, if training using Italian, Spanish, Romanian, and Turkish). Ideally, we want something in-between pairwise and universal models.
- Per-Language Encoder/Decoder: Use a separate encoder and a separate decoder for each language. This results in a total of \(LP\) parameters and lies somewhere between the pairwise and the universal approaches. However, no information can be shared between languages that are similar (e.g., Italian and Spanish).
At EMNLP 2018, we introduced the contextual parameter generator (CPG), a new way to share information across different languages that generalizes the above three approaches, while mitigating their issues and allowing explicit control over the amount of sharing.
Contextual Parameter Generation
Let us denote the source language for a given sentence pair by \(\ell_s\) and the target language by \(\ell_t\). When using the contextual parameter generator, the parameters of the encoder are defined as \(\theta^{(enc)}\triangleq g^{(enc)}({\bf l}_s)\), for some function \(g^{(enc)}\), where \({\bf l}_s\) denotes a language embedding for the source language \(\ell_s\). Similarly, the parameters of the decoder are defined as \(\theta^{(dec)}\triangleq g^{(dec)}({\bf l}_t)\) for some function \(g^{(dec)}\), where \({\bf l}_t\) denotes a language embedding for the target language \(\ell_t\). Our general formulation does not impose any constraints on the functional form of \(g^{(enc)}\) and \(g^{(dec)}\). In this case, you can think of the source language, \(\ell_s\), as a context for the encoder. The parameters of the encoder depend on its context, but its architecture is common across all contexts. We can make a similar argument for the decoder, and that is where the name of this parameter generator comes from. We can even go a step further and have a parameter generator that defines \(\theta^{(enc)}\triangleq g^{(enc)}({\bf l}_s, {\bf l}_t)\) and \(\theta^{(dec)}\triangleq g^{(dec)}({\bf l}_s, {\bf l}_t)\), thus coupling the encoding and decoding stages for a given language pair. This would make the model more expressive and could thus work better in cases where large amounts of training data are available. In our experiments we stick to the previous, decoupled, form, because it has the potential to lead to a common representation among languages, also known as an interlingua. An overview diagram of how the contextual parameter generator fits in the architecture of NMT models is shown in Figure 1 in the beginning of this post.
Concretely, because the encoding and decoding stages are decoupled, the encoder is not aware of the target language while generating it, and so, we can take an encoded intermediate representation of a sentence and translate it to any target language. This is because the intermediate representation is independent of any target language. This makes for a stronger argument that the intermediate representation produced by our encoder could be approaching a universal interlingua, more so than methods that are aware of the target language when they perform encoding.
Parameter Generator Network
We refer to the functions \(g^{(enc)}\) and \(g^{(dec)}\) as parameter generator networks. A simple form that works, and for which we can reason about, is to define the parameter generator networks as simple linear transforms:
$$g^{(enc)}({\bf l}_s) \triangleq {\bf W^{(enc)}} {\bf l}_s,$$
$$g^{(dec)}({\bf l}_t) \triangleq {\bf W^{(dec)}} {\bf l}_t,$$
where \({\bf l}_s, {\bf l}_t \in \mathbb{R}^M\), \({\bf W^{(enc)}} \in \mathbb{R}^{P^{(enc)} \times M}\), \({\bf W^{(dec)}} \in \mathbb{R}^{P^{(dec)} \times M}\), \(M\) is the language embedding size, \(P^{(enc)}\) is the number of parameters of the encoder, and \(P^{(dec)}\) is the number of parameters of the decoder.
Another interpretation of this model is that it imposes a low-rank constraint on the parameters. As opposed to our approach, in the base case of using multiple pairwise models to perform multilingual translation, each model has \(P = P^{(enc)} + P^{(dec)}\) learnable parameters for its encoder and decoder. Given that the models are pairwise, for \(L\) languages, we have a total of \(L(L - 1)\) learnable parameter vectors of size \(P\). On the other hand, using our contextual parameter generator we have a total of \(L\) vectors of size \(M\) (one for each language), and a single matrix of size \(P \times M\). Then, the parameters of the encoder and the decoder, for a single language pair, are defined as a linear combination of the \(M\) columns of that matrix, as shown in the above equations. In our EMNLP 2018 paper, we consider and discuss more options for the parameter generator network, that allow for controllable parameter sharing.
Generalization
The contextual parameter generator is a generalization of previous approaches for multilingual NMT:
- Pairwise: \(g\) picks a different parameter set based on the language pair.
- Universal: \(g\) picks the same parameters for all languages.
- Per-Language Encoder/Decoder: \(g\) picks a different set of encoder/decoder parameters based on the languages.
Semi-Supervised and Zero-Shot Learning
The parameter generator also enables semi-supervised learning. Monolingual data can be used to train the shared encoder/decoder networks to translate a sentence from some language to itself (similar to the idea of auto-encoders). This is possible and can help learning because many of the learnable parameters are shared across languages.
Furthermore, zero-shot translation, where the model translates between language pairs for which it has seen no explicit training data, is also possible. This is because the same per-language parameters are used to translate to and from a given language, irrespective of the language at the other end. Therefore, as long as we train our model using some language pairs that involve a given language, it is possible to learn to translate in any direction involving that language.
Potential for Adaptation
Let us assume that we have trained a model using data for some set of languages, \(\ell_1, \ell_2, \dots, \ell_m\). If we obtain data for some new language \(\ell_n\), we do not have to retrain the whole model from scratch. In fact, we can fix the parameters that are shared across all languages and only learn the embedding for the new language (along with the relevant word embeddings if not using a shared vocabulary). Assuming that we had a sufficient number of languages in the beginning, this may allow us to obtain reasonable translation performance for the new language, with a minimal amount of training (due to the small number of parameters that need to be learned in this case --- to put this into perspective, in most of our experiments we used language embeddings of size 8).
Number of Parameters
For the base case of using multiple pairwise models to perform multilingual translation, each model has \(P + 2WV\) parameters, where \(P = P^{(enc)} + P^{(dec)}\), \(W\) is the word embedding size, and \(V\) is the vocabulary size per language (assumed to be the same across languages, without loss of generality). Given that the models are pairwise, for \(L\) languages, we have a total of \(L(L - 1)(P + 2WV)\)\(=\mathcal{O}(L^2P +2L^2WV)\) learnable parameters. For our approach, using the linear parameter generator network we have a total of \(\mathcal{O}(PM + LWV)\) learnable parameters. Note that the number of encoder/decoder parameters has no dependence on \(L\) now, meaning that our model can easily scale to a large number of languages.
For putting these numbers into perspective, in our experiments we had \(W = 512\), \(V = 20000\), \(L = 8\), \(M = 6\), and \(P\) in the order millions.
Results
We present results from experiments on two datasets in our paper, but here we highlight some of the most interesting ones. In the following table we compare CPG to using the pairwise NMT models approach, as well as the universal one (using Google's multilingual NMT system). Below are results for the IWSLT-15 dataset, a commonly used small dataset in NMT community.
| Pairwise | Universal | CPG | |
|---|---|---|---|
| En-Cs | 14.89 | 15.92 | 17.22 |
| Cs-En | 24.43 | 25.25 | 27.37 |
| En-De | 25.99 | 25.92 | 26.77 |
| De-En | 30.93 | 29.60 | 31.77 |
| En-Fr | 38.25 | 34.40 | 38.32 |
| Fr-En | 37.40 | 35.14 | 37.89 |
| En-Th | 23.62 | 22.22 | 26.33 |
| Th-En | 15.54 | 14.03 | 26.77 |
| En-Vi | 27.47 | 25.54 | 29.03 |
| Vi-En | 24.03 | 23.19 | 26.38 |
| Mean | 26.26 | 25.12 | 27.80 |
The numbers shown in this table represent BLEU scores, the most widely used metric for evaluating MT systems. They represent a measure of precision over \(n\)-grams. More specifically, in this instance they represent a measure of how frequently the MT prediction outputs 4 consecutive words that match 4 consecutive words in the reference translation.
We show similar results for the IWSLT-17 dataset (commonly used challenge dataset for multilingual NMT systems that includes a zero-shot setting) in our paper, where CPG outperforms both the pairwise approach and the universal approach (i.e., Google's system). Most interestingly, we computed the cosine distance between all pairs of language embeddings learned by CPG:
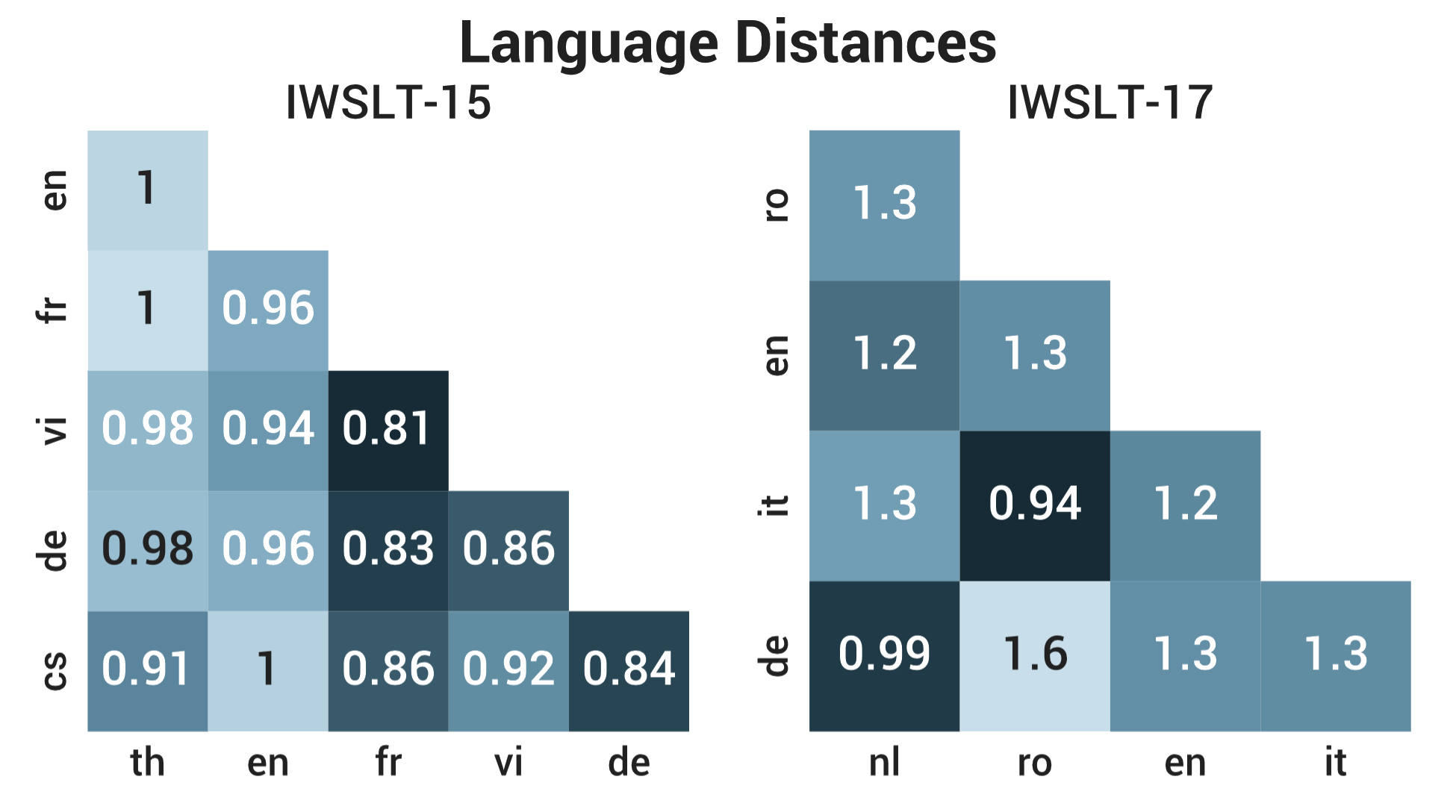
Figure 6: Cosine distance between all pairs of the language embeddings learned using our contextual parameter generator. Note that the cosine distance values can range between 0 and 2.
There are some interesting patterns that indicate that the learned language embeddings are reasonable. For example, we observe that German (De) and Dutch (Nl) are most similar for the IWSLT-17 dataset, with Italian (It) and Romanian (Ro) coming second. Furthermore, Romanian and German are the furthest apart for that dataset. It is very encouraging to see that these relationships agree with linguistic knowledge about these languages and the families they belong to. We see similar patterns in the IWSLT-15 results but we focus on IWSLT-17 here, because it is a larger, better quality dataset with more supervised language pairs. These results also uncover relationships between languages that may have been previously unknown. For example, perhaps surprisingly, French (Fr) and Vietnamese (Vi) appear to be significantly related for the IWSLT-15 dataset results. This is likely due to French influence in Vietnamese due to the occupation of Vietnam by France during the 19th and 20th centuries.
Where should you look to learn more?
More details can be found in our EMNLP 2018 paper. We have also released an implementation of our approach and experiments as part of a new Scala framework for machine translation. It is built on top of TensorFlow Scala and follows a modular NMT design that supports various NMT models, including our baselines. It also contains data loading and preprocessing pipelines that support multiple datasets and languages, and is more efficient than other packages (e.g., tf-nmt). Furthermore, the framework supports various vocabularies, among which we provide a new implementation for the byte-pair encoding (BPE) algorithm that is 2 to 3 orders of magnitude faster than the released one.
I also plan to release another blog post later on in 2019 with some follow-up work we have done on applying contextual parameter generation to other problems.
Acknowledgements
We would like to thank Otilia Stretcu, Abulhair Saparov, and Maruan Al-Shedivat for the useful feedback they provided in early versions of this paper. This research was supported in part by AFOSR under grant FA95501710218.
References
Emmanouil Antonios Platanios, Mrinmaya Sachan, Graham Neubig, and Tom Mitchell. 2018. Contextual Parameter Generation for Universal Neural Machine Translation. In Conference on Empirical Methods in Natural Language Processing (EMNLP), Brussels, Belgium.
Orhan Firat, Kyunghyun Cho, and Yoshua Bengio. 2016a. Multi-Way, Multilingual Neural Machine Translation with a Shared Attention Mechanism. In Proceedings of NAACL-HLT, pages 866–875.
Thanh-Le Ha, Jan Niehues, and Alexander Waibel. 2016. Toward Multilingual Neural Machine Translation with Universal Encoder and Decoder. In Proceedings of the 13th International Workshop on Spoken Language Translation.
Melvin Johnson, Mike Schuster, Quoc V Le, Maxim Krikun, Yonghui Wu, Zhifeng Chen, Nikhil Thorat, Fernanda Viegas, Martin Wattenberg, Greg Corrado, et al. 2017. Google’s Multilingual Neural Machine Translation System: Enabling Zero-Shot Translation. In Transactions of the Association for Computational Linguistics, volume 5, pages 339–351.
Minh-Thang Luong, Quoc V Le, Ilya Sutskever, Oriol Vinyals, and Lukasz Kaiser 2016. Multi-task Sequence to Sequence Learning. In International Conference on Learning Representations.
Orhan Firat, Kyunghyun Cho, and Yoshua Bengio. 2016a. Multi-Way, Multilingual Neural Machine Translation with a Shared Attention Mechanism. In Proceedings of NAACL-HLT, pages 866–875.
Thanh-Le Ha, Jan Niehues, and Alexander Waibel. 2016. Toward Multilingual Neural Machine Translation with Universal Encoder and Decoder. In Proceedings of the 13th International Workshop on Spoken Language Translation.
Melvin Johnson, Mike Schuster, Quoc V Le, Maxim Krikun, Yonghui Wu, Zhifeng Chen, Nikhil Thorat, Fernanda Viegas, Martin Wattenberg, Greg Corrado, et al. 2017. Google’s Multilingual Neural Machine Translation System: Enabling Zero-Shot Translation. In Transactions of the Association for Computational Linguistics, volume 5, pages 339–351.
Minh-Thang Luong, Quoc V Le, Ilya Sutskever, Oriol Vinyals, and Lukasz Kaiser 2016. Multi-task Sequence to Sequence Learning. In International Conference on Learning Representations.